
Their should be no shame nowadays SCORE 122
Student debt payments SCORE 8

How Most Of My Friendships Work SCORE 121

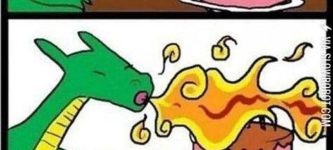
Tiny Roar SCORE 12

You are diagnosed with SFD SCORE 184

English In China SCORE 159

Incredibly Well-Timed Shot SCORE 15

Precious SCORE 193
When you think you are smart. SCORE 188

How Do You Have Friends? SCORE 113

Awesome Ice Age’s Scrat Cake SCORE 15

Best Costume Idea Ever SCORE 213

Sleep tight pupper SCORE 1

Sit anywhere with this invention SCORE 125

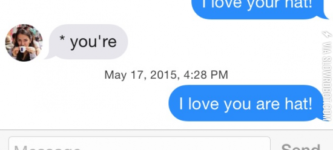
I would read the f*ck out of this SCORE 138

Difference between a master and a beginner SCORE 166

You could kick a field goal through those chompers. SCORE 14

Something I’ve Never Thought About Before SCORE 198

Religious Wars Explained SCORE -3

Every Time I Go To An Expensive Restaurant SCORE 16

Happy 30th birthday, Mario! SCORE 14

Give It A Few Years. SCORE 123

I can relate to this SCORE 137

Classic Disney Movies In Real Life SCORE 12

Just Don’t Wake Me Up SCORE 12

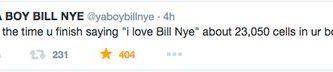
Bill Nye the Science Guy in science class. SCORE 16

An Amputee Pretends To Be A Zombie And Chases A Guy. SCORE 177

Most Evil Villain Ever SCORE 166

Choo-choo SCORE 234

Complicated Medication Instructions SCORE 113

Clever Japanese Architecture SCORE 12
Fun fact of the day SCORE 6
